Unsented 칼만 필터

AUTHOR: Sungwook LE
DATE: ‘21.9/18
Book: 칼만필터의 이해, 김성필
Implementation Code: My Code
Refernece: 블로그 참고 This

• Extended 칼만 필터가 선형 알고리즘을 자연스럽게 확장해 Nonlinear 문제를 해결했다면, Unscented Kalman Filter는 발상의 전환을 통해 아예 선형화 과정을 생략하는 접근법
• 따라서, Unscented 칼만 필터는 Jacobian 으로 구한 선형 모델 때문에 불안정해지는 문제에서 자유롭다.

1. Introduction

1. x -> x' 으로 $f(x)$ 비선형 transformation을 한다. 이 때, 새로운 $x’$의 위치와 분산은 어떻게 예측할 수 있을까?
   • 이름에서도 적혀있듯, Unsecented 칼만 필터의 핵심 기반은 Unscented 변환: Unscented Transformation이다.
   • Unscented 변환은 몬테카를로 시뮬레이션과 비슷한 개념
   • 다만, Monte Carlo 방식이 무작위 샘플을 추출하는 것이라면, Unscented 변환은 샘플과 각 샘플의 가중치를 정교하교 선정
   • 따라서, 몬테카를로 방식보다 훨씬 적은 수의 샘플로 유효한 표준과 공분산 예측 시뮬레이션 가능하다는 장점이 있는 것이 Unscented 이다.
2. 칼만 문제로 돌아와서 생각해보자

   • Extended 칼만 필터는 아래와 같은 접근법이다. $x_k = f(x_{k-1})$ $P_k = AP_{k-1}A^T + Q $ 여기서 A는 Jacobian 선형화를 한 값으로, 선형화 이후엔 Linear 칼만필터와 동일하게 진행

   • f(x)의 Jacobian없이 오차 공분산을 예측하는 방법의 해결책이 Unscented 변환이다.

   • Jacobian 연산으로 분산을 예측하지 않고, x의 평균과 공분산에 맞춰 시그마포인트(샘플)를 선정하고, 이 시그마 포인트를 f(x)로 변환

   • 새로운 시그마 포인트 $f(\chi)$ 에 대해 가중 평균과 가중 공분산을 계산한다. 이 값이 바로 $f(x)$의 평균과 공분산이 된다.

     
   • 아래 그림을 통해 EKF VS UKF의 차이점을 살펴보면, EKF는 비선형을 선형화 하여 보라색(분산) 으로 예측하였지만 UKF의 초록색(분산) 은 Unscented Transformation (샘플을 통한 계산)을 통해 선정되었다. 즉, 빨간색 샘플들의 비선형 이동을 보고 그 값들의 분산을 새로운 분산으로 예측하였다는 것에 차이점이 있다.
   
   • 아래 그림은 EKF Vs, Particle Filter Vs. UKF의 차이점을 보여준다.
   

2. 내용

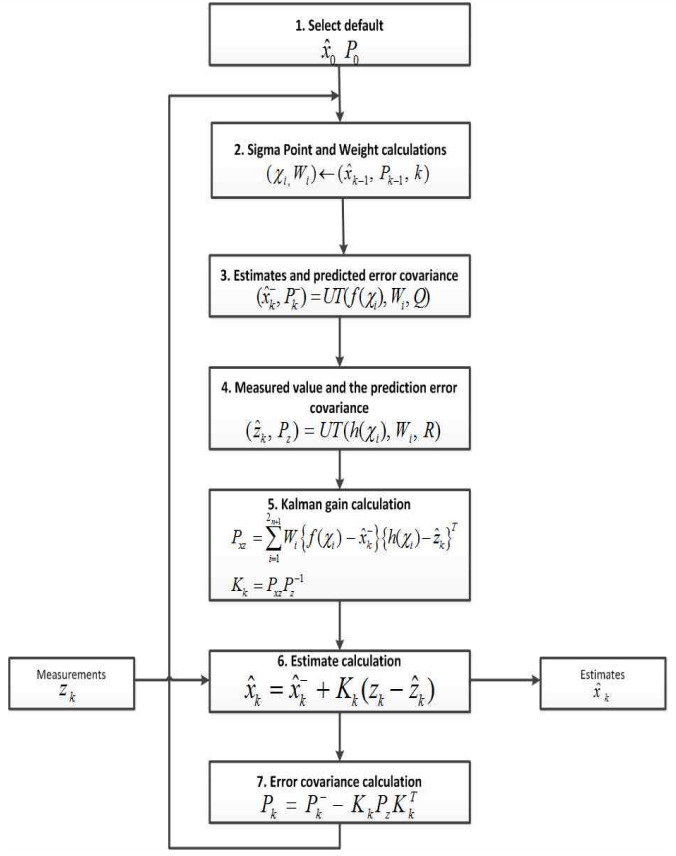
UKF 또한 다른 칼만 시리즈와 마찬가지로 예측 -> 칼만 게인 -> 추정의 단계는 동일하다.

2-1. FLOW

1. UKF: 비선형 문제를 푸는 데 있어서, SigmaPoints(샘플), Sample Weight 을 구하고, UT(Unscented Trnasformation) 수행의 결과로 나온 값을 기준으로 예측한다.
2. UKF: 칼만 게인 구하는 데 있어, SigmaPoints(샘플) 의 UT(Unscented Trnasformation) 을 이용하여 $f(\chi)$ 와, $h(\chi)$ 를 구하고, 분산을 업데이트한다. 이 값을 이용하여 Kalman Gain을 구한다.
3. UKF: 마지막 추정 단계는 다른 칼만 필터와 동일하다.

   2-2. Unscented Transform

   UKF가 비선형성을 표현하는 방식은 Unscented Transform을 이용한다. UT는 세가지로 구성되는데, 첫번째는 SigmaPoints 선택이요, 두번째는 샘플들의 가중치 선택, 세번째는 새로운 가우시안 분포 계산(평균, 분산)이다.

   • 칼만 분산을 근거로 샘플를 선택하는 방법: (SigemaPoints)
   • 칼만 분산을 근거로 선택된 샘플들의 가중치 선택 (Weight Selection)
   • SigmaPoints, Weight를 이용한 평균값과 분산을 eEquation계산하는 방법

2-2-1. Sigma point selection

Unscented transform을 하기 위해서는 가장 먼저 sigma point를 선정해야 한다. 시그마 포인트는 $\chi$로 표기하며 다음과 같이 선택한다.

$χ[0]=μ $

$ χ[i] =μ$

$ χ[i]=μ+(\sqrt{(n+\kappa)Σ})^i \space for \space i=1,⋯,n$

$ χ[i]=μ−(\sqrt{(n+\kappa)Σ})^{i−n} \space for \space i=n+1,⋯,2n$

• 위 식에서 n은 dimension의 크기며, $\lambda$는 scaling parameter이다. $()^{i}$는 covariance matrix의 i번째 열 vector를 의미한다.
• 첫번째 sigma point는 평균(mean) vector가 되며, 그 다음 sigma point는 dimension의 크기에 따라서 갯수가 결정된다. 2-dim 일 경우에는 4개의 point가 추가되어 총 5개가 되며, 3-dim인 경우에는 6개가 추가되어 총 7개가 된다.

• Sigma point를 계산하는 식에 covariance matrix(Σ)의 square root를 계산해야 하는데, matrix의 square root는 Cholesky Factorization**을 이용한다. 분산 매트릭스의 sqrt를 하기 위해 필요한 매트릭스 분해 연산이다.

• 여기서 $\kappa$는 하이퍼파라미터인데, 값이 클 수록 샘플들을을 멀리 배치하게 됨을 볼 수 있다. Sigma point가 mean값과 매우 가까운 경우는 Taylor expansion을 통한 선형화와 유사하며, 너무 먼 경우는 비선형 함수를 재대로 반영하지 못하므로 적당한 값을 적용해야 한다.

2-2-2. Weight Selection

선택된 Sigma point들은 각각 weight를 갖고 있으며, Gaussian 분포를 다시 계산할 때 사용된다. Weight의 합은 1이 되며$(\Sigma \omega^{[i]} =1)$ 다음과 같이 정의한다.

$ ω_m^{[0]}​=\frac{\kappa}{n+\kappa}$

$​ω_m^{[i]}=ω_c^{[i]}=\frac{1}{2(n+\kappa)} \space for \space i=1,⋯,2n$

2-2-3. Gaussian Distribution Calculation

위의 과정을 통해 dimension에 맞는 sigma points 들과 weight가 계산되었다. 이제 계산된 sigma point들을 비선형 함수(g(x))의 입력으로 사용하고, 비선형 함수의 출력을 이용하여 Gaussian 분포를 추정한다. 출력 Gaussian 분포의 mean과 covariance는 다음과 같이 계산된다.

$μ^′= ∑_{i=0}^{2n} ω_m^{[i]}​g(χ[i])$

$Σ^′= ∑_{i=0}^{2n} ω_c^{[i]}(g(χ[i])−μ^′)(g(χ[i])−μ^′)^T​$

3. 구현

구현 문제: 롤레이트, 피치레이트, 요레이트 센서를 이용한 드론의 자세 추정/예측
추정 필요 State: 롤, 피치 앵글
센서 measure: 롤, 피치 앵글 계측됨

1) State
$x=\left [\begin{array}{lcr} \phi \\
\theta \\
\varphi \end{array} \right] <\phi=roll, \theta=pitch, \varphi=yaw>$

2) System Model(Non-linear)

$\left [\begin{array}{} \dot\phi \\
\dot\theta \\
\dot\varphi \end{array} \right]= \left [\begin{array}{} 1 & sin\phi tan\theta & cos\phi tan\theta \\
0 & cos\phi & -sin\phi \\
0 & sin\phi sec\theta & cos\phi sec\theta \end{array} \right] \left [\begin{array}{} p \\
q \\
r \end{array} \right] + w =f(x)+w $ $ <sensor \space measured: p=roll rate, q=pitch rate, r=yaw rate>$

3) Output equation

$z=\left [\begin{array}{} 1 & 0 & 0 \\
0 & 1 & 0 \end{array} \right]\left [\begin{array}{} \phi \\
\theta \\
\varphi \end{array} \right] +v = h(x)+v $

3-1. Code

• Eigen Library를 이용하여 구현
• 코드 구현: My Code is Here
• 코드에선 아래 4개 method를 UKF의 iterative process로 하여 구현하였다.

UKF.SigmaPoints_WeightSelect();
UKF.Predict(measured);
UKF.KalmanGainCalculation();
UKF.Update(measured);

4. Conclusion

1. UKF Vs. EKF
   • UKF와 EKF 비교
   • 선형 모델에서는 EKF와 UKF의 결과는 같다.
   • 비선형 모델에서는 UKF가 EKF보다 더 나은 근사화 방법을 사용한다.
   • 하지만 결과의 차이는 많은 경우에 그다지 크지 않다.
   • UKF는 Jacobian matrix를 구할 필요가 없다.
   • 계산 복잡도는 비슷하며, UKF가 EKF보다 계산속도는 약간 더 느리다.

2. UKF 는 정교하게 선택한 샘플(SigmaPoints)들을 비선형성을 계산하고 새로운 분산과 평균을 계산해냄으로써, 비선형성을 비선형성 그대로 풀 수 있다.

3. $\kappa$ 의 선택에 따라 $\kappa$가 작다면 EKF와 동일할 것이고 $\kappa$가 크다면 비선형성을 제대로 표현하는데 한계가 발생하므로, 적절한 $\kappa$ 선택이 필요하다.

4. Unscented 칼만 필터는 비선형 함수 자체를 모사하는 것보다는 이 함수의 확률 분포를 모사하는 게 더 낫다는 전략에 따라 고안된 비선형 칼만 필터이다. 다시 말해 비선형 함수를 근사화한 선형 함수를 찾는 대신 비선형 함수의 평균과 공분산을 근사적으로 직접 구하는 전략을 사용한다.

5. Unscented 칼만 필터는 자코비안을 이용한 선형 모델이 불안정하거나 구하기 어려운 경우에 확장 칼만 필터의 좋은 대안이 된다.

끝