Kalman Filter: Essential

Kalman Filter: Essential

AUTHOR: SungwookLE
DATE: ‘21.9/12
LECTURE: Udacity Lecture
PAPER: Discrete system 차량 상태 추정

1. Introduction

시작하기 전에, 짧게 추정기(Estimator)와 필터(Filter)에 대해 간략하게 이야기 해보고자 한다. Estimator는 Observer(관측기)와 Estimator(추정기)로 나뉠 수 있는데, Observer의 경우 hidden state에 대한 observability가 있는 케이스를 말한다. 즉, 초기값과 관계없이 내가 추정하고자하는 state를 추정할 수 있으면 observer이고, 그렇지 못하면 estimator이다. 후자의 경우 filter라고 부를 수 있는데, 예를 들면 Low-Pass Filter는 신호의 Noise를 제거하는 역할을 수행할 뿐, 신호의 참값을 추정한다고 보긴 어렵다. 이런 경우 Noise를 제거하는 Filter의 역할만을 수행하는 것이다.
칼만필터는 잘 알려진 추정기(Estimator)이자, 확률 필터(Filter)이다. 두가지 분야 사용할 수 있다는 의미이다. 본 글을 통해 선형 칼만필터를 정리해보자.
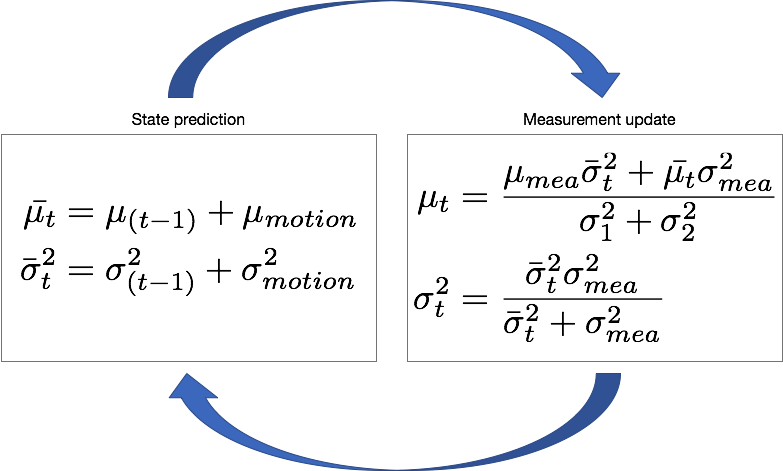
칼만 필터는, 아래와 같이 2가지 단계로 이루어져 있다. 첫번째는 모델을 이용하여 값을 예측하는 State Prediction단계와 두번째는 측정값을 이용하여 값을 보정하는(업데이트) Measurement Update단계이다. 여기서 값은 상태변수(State) 이다. 핵심이 되는 컨셉을 아래의 문장으로 적어 보았다.

모델의 불확실성(분산Q)과 측정의 불확실성(분산R)을 고려하여 모델로 계산한 state1와 측정값을 통해 계산된 state2의 Weighted Mean 값을 최종 state로 출략한다.

위 그림은 확률 개념으로 설명된 칼만필터의 구조이다. State Prediction 과 Measurement Update로 이루어져 있는 것을 확인하자. 칼만필터를 통해 계산된 출력값은 Measure와 State Model의 분산의 역수의 정규화된 값을 가중치로 하는 평균임을 알 수 있다. (출력값: State, 위 그림에선 $\mu_t$)

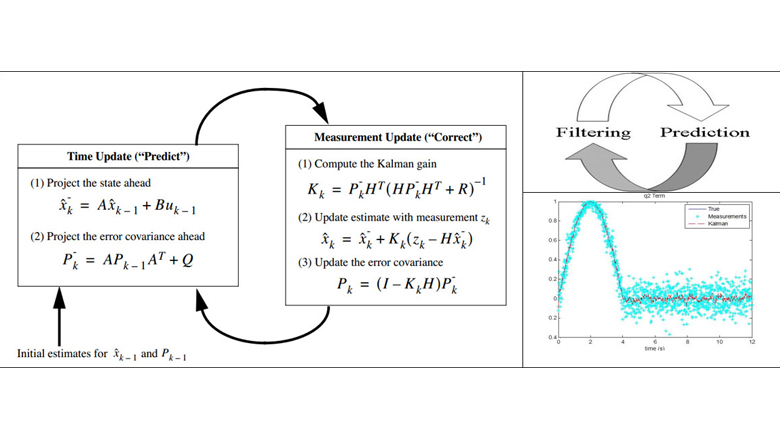
위 그림은 유도된 칼만필터의 전체식을 보여주고 있다. Linear System으로 표현된 상태 공간에서의 수식유도라 바로 위그림의 확률 수식과 달라보이지만, 정확히 같은 수식이다. PAPER의 차량 상태 추정기들을 살펴보면 위의 수식에 따라 유도되어 사용하고 있음을 알 수 있다. 해당 논문은 Extended Kalman Filter이나, 같은 수식으로 이해해도 무방하다.

2. Kalman Derivation

상기 컨셉을 수식으로 유도하는 방식은 여러가지 방법이 있는데, 본 글에서는 2가지 방식을 짧게 소개한다. 2가지 방식으로 유도한 수식은 동일한 값으로 칼만필터의 수식이 된다.

2-1. 최적화 접근법

목적함수를 최소로 하는 게인 K 구하기

확률적 접근법이 아닌 최적화이론 접근법으로 정의된 2차 함수 형태를 갖는 목적함수의 1차 미분값이 0이 되게 하는 최적 게인을 구하는 문제가 칼만 필터의 설계 방법이다. 이러한 칼만 필터의 목적함수 형태를 이해하고 있으면, 칼만 필터 하이퍼 파라미터 튜닝에 용이하다. 칼만 필터의 하이퍼 파라미터는 모델의 분산(Q)와 측정 분산(R), 칼만 시스템 분산(P)이다.

보정단계에서의 목적함수(Cost function)
$J_m$ $ =0.5(y_k−h({x_k}))^TR^{-1}(y_k−h(x_k))$ $ +0.5(x_k−f(x_{k−1}))^T$ $ P_{k|k−1}^{−1}$ $ (x_k−f(x_{k−1}))$

해당 수식의 목적함수 Jm은 업데이트 단계에서의 목적함수를 나타낸다. 업데이트 단계에서는 보정(Correction) 값을 계산하기 위해 최적 게인 K를 계산하고 추정 에러의 차이만큼 K배 보정하여 최종 state값을 출력한다.
목적함수 수식을 살펴보자. 1번째 Term은 측정값과 현재값의 에러로서 가중치를 측정 분산의 역수로 선언했고, 2번째 Term은 현재 값과 모델 예측값의 에러로서 가중치는 분산 P의 역수로 선언했다. P에는 모델 분산 Q가 더해져 있다. R이 크다는 것은 센서의 오차가 크다는 의미이고 이런 경우 측정 에러(y-h(x))의 가중치를 낮게두어야지만 적절한 보정값 계산에 도움이 된다. 즉, 측정 분산 R이 크면 모델 예측값에 (상대적) 가중치를 더 주어 모델 예측값에 의존하게 되고, 모델 분산 Q가 크면 측정 값에 (상대적) 가중치를 두어 최종 state를 계산하게 된다.
칼만필터를 튜닝할 때, P,Q,R 각 분산값을 조정하게 되는데 목적함수의 가중치를 조절하는 것이 된다.P값은 초기 추정 속도에 영향을 주는데 P값이 클 수록 초기에 측정값에 가중치를 두게 되어, 초기값을 모르는 상태(초기값은 보통 0으로 둔다)에서 센서의 값에 의존하게 하여 초기 추정 속도를 빠르게 하는 역할을 한다.
수식 유도는, 해당 목적함수가 최소화 되게 하는 게인 K를 유도하는 과정이다. 목적함수는 2차 함수 형태이므로, 1차 미분이 0이 되게 하는 게인 K를 구하면 되고, 위의 목적함수에서 K는 직접적으로 보이진 않으나, P 안에 존재한다.

2-2. 확률통계 접근법

확률이론(total probability & Bayes Rule)을 통한 상태값 추론

prediction(forward): total probability 확률 이론
update(correction): bayes rule 확률 이론

확률이론이라고 거창하게 썼지만, 사실상 Weighted Mean개념만 이해하면 된다. Weighted Mean이라는 단어에서도 볼 수 있듯이 Weighted 계수가 있어야 하는데, 이 때 사용하는 Weighted 계수가 바로 각각 모델(prediction) 단계에서의 분산(Q)의 역수와 측정(measurement)단계에서의 분산(R)의 역수이다.
업데이트 단계에서의 출력 값(Bayes Rule) 업데이트 단계에서 측정값을 가지고 보정을 하게 되는데, 측정값은 P(z|x)이고, 우리가 알고 싶어하는 값은 P(x|z)이므로 Bayes Rule을 이용하여 구하게 된다.

P(x|z) = P(z|x) * P(x) / P(z)

최종적으로 출력하게 될 state의 확률은 측정값과 모델 예측값의 중간 어디쯤에 존재하고 있으니,
두 값의 중간 분산값을 기준으로 하여 Normalized하여 계산한 값 (다시 말해, weighted mean)이 P(x|z)이다.

$P(x|z) = P(z|x) * P(x) / P(z)$ $ = P(z|x) * P(x) / (1/R+1/Q)$ $ = P(z|x_{pred}) * P(x_{pred}) + P(z|x_{measure}) * P(x_{measure}) / (1/R+1/Q)$ $ = x_{pred} * P(x_{pred}) + x_{measure} * P(x_{measure}) / (1/R+1/Q)$ $ = (x_{pred} * 1/Q + x_{measure} * 1/R) / (1/R+1/Q) $

1) 출력 State

$X_{new} = {(X_{pred} * 1 / Q + X_{meas} * 1/R)} / {(1/Q + 1/R)}$
$X_{new} = {(X_{pred} * R + X_{meas} * Q)} / {(Q+R)}$

2) 칼만 시스템 분산 P

$P_{new} = \frac{1}{(1/R + 1/Q)}$
$P_{new} = \frac{RQ}{(R+Q)}$

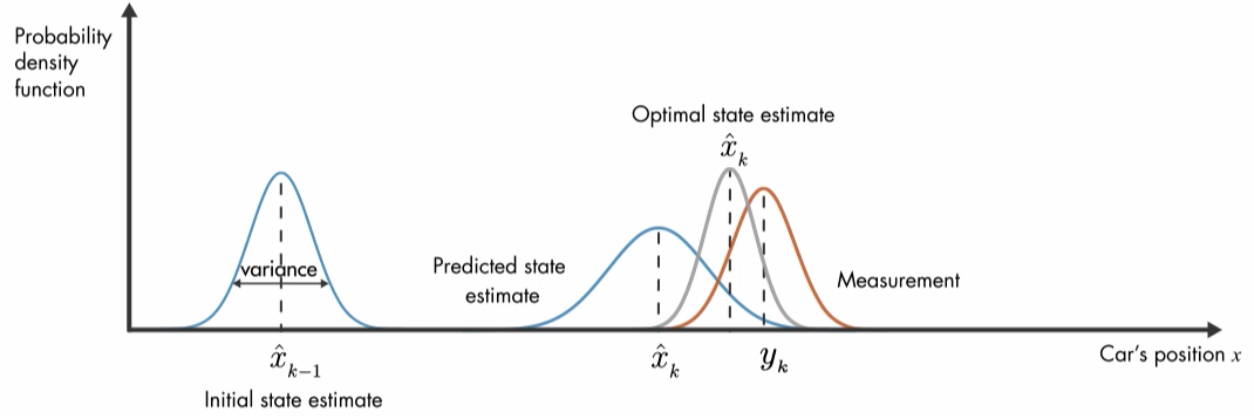위 그림과 같이 보정단계에서 새로운 state는 모델과 측정값의 분산값을 기준으로 weighted mean 되고 이 수식은 bayes rule을 이용하여 유도한 것이다.

업데이트가 진행됨에 따라 분산값은 점점 작게 업데이트 되며 수렴하게 된다. (확률 추론 과정)

예측 단계에서의 출력 값(Total Probability) 전확률 법칙이라는 것은 칼만 시스템에 적용하면 새로이 입력된 input(현재 시간 기준)이 들어옴에 따라 예측하여야할 시스템에 불확실성이 더해짐을 말한다. input이 들어옴에 따라, 전체 P(x)는 더해지기만 하였다. Markov Process 관점에서 살펴보면 B1, B2, B3은 각각의 Markov chain에서의 시간 흐름이라고 보면 되고, 현재의 input 이 들어올 때마다 전체 모집단의 크기에 불확실성은 더해주어야 한다. 다만 칼만시스템에서 P가 무한히 커지지 않고 수렴하는 것은 업데이트(보정)단계에서 보정이 이루어지기 때문이다.

1) 출력 State

$X = X + f(x,input)*dt$

2) 칼만 시스템 분산 P

$P = APA^T + Q$ 시스템행렬 (dot_x = Ax+Bu 에서 A)이 분산의 변화에도 영향을 주기 때문에 수식은 위와 같이 구성되는데, A 가 1이라고 치고 쉽게 쓰자면 아래와 같다. $P = P+Q$

3. Implementation

c++ 구현! 칼만필터는 효과적인 최적(강건) 필터이면서 동시에 구현도 쉽다.

3-1. Single State Kalman Filter

1차원 선형 칼만, 흔히 보는 칼만 필터 수식 형태가 아니고 분산의 가중치 평균을 이용하여 값을 보정하는 형태로 수식을 작성하였다. 수식의 형태만 다를 뿐 System Mtx A=1 이고, input Mtx B =1, Output Mtx C =1인 칼만필터와 정확히 같다.

아래 구현 문제:
왼쪽(-) 또는 오른쪽(+)으로 움직일 수 있는 로봇이 있다. 로봇은 input만큼 움직일 수 있고, 로봇의 위치는 센서로 측정되어 measure된다. 로봇의 위치 추정 필터를 설계하여라.

template <typename T>
class Kalman{
    public:
    Kalman(T covariance_measurement_, T covariance_prediction_){
        covariance_measurement = covariance_measurement_;
        covariance_prediction = covariance_prediction_;
    }

    void measure_upate(T mean_measure){
        // 베이즈 법칙에 따라 조건부확률에 따라 업데이트 된다.
        T mean_now = mean;
        T covariance_now = covariance;


        T new_covariance = 1/(1/covariance_now+ 1/covariance_measurement );
        T new_mean = (mean_now * 1/covariance_now + mean_measure*1/covariance_measurement)
                     / (1/new_covariance);

        mean = new_mean;
        covariance = new_covariance;

        std::cout << "update: " << "[" << mean << "," <<covariance << "]" << std::endl;

    }

    void model_prediction(T input){
        //input 이 들어옴에 따라 전확률 법칙에 의거하여 전체 분산은 (+)가 된다.
        mean = mean + input;
        covariance = covariance + covariance_prediction ;

        std::cout << "predict: " << "[" << mean << "," <<covariance << "]" << std::endl;
    }

    private:
    T covariance_measurement;
    T covariance_prediction;
    T mean=0;
    T covariance=1000.0;
};

int main(){

    std::vector<double> inputs={1,1,2,1,1};
    std::vector<double> measurements={5,6,7,9,10};

    double measure_cov = 4;
    double model_cov = 2;

    Kalman<double> kf(measure_cov, model_cov);

    for(int i =0 ; i < measurements.size(); ++i){
        kf.measure_upate(measurements[i]);
        kf.model_prediction(inputs[i]);
    }

    return 0;
}

3-2. Multi State Kalman Filter

hidden state (observable) 다차원의 State를 추정할 때, 모든 State를 추정할 수 있는 것은 아니다. 나는 추정기와 필터를 구분하여 부르는 것을 선호하는데, 추정기는 observability가 있어 측정값으로 내가 구하고자 하는 state를 초기값과 관계없이 추정할 수 있는 관측기를 의미하고(observer), 필터는 observability가 없어 state의 노이즈를 제거하는(예시: moving sum filter) 역할만을 수행하는 것을 말한다. 이런 경우 초기값의 오차는 극복이 안되고 costant error로 존재하게 된다.
예를 들어보면, 속도만으로 위치를 추정하고자 할 때, 초기 위치를 모르면 추정한 위치는 내가 설정한 초기 위치와 물체의 실제 초기위치 만큼의 초기 에러가 존재하는데 이는 constant error로 남게 된다. observability는 선형시스템 이론을 참고하길 바란다. dot_x = Ax+bu, y=Cx로 이루어진 선형 시스템에서 A와 C mtx간의 rank 관계를 통한 observable information 여부(observability)는 어떻게 확인할 수 있고 개선될 수 있는지 배울 수 있다.
hidden state는 observable 관계를 이용하여 추정할 수 있는 state를 말하고 추정기는 대부분 센서로 계측이 되지 안흔ㄴ 경우에 필요한 경우가 많아서, 우리가 필터가 아닌 추정기를 설계할 떄는 대부분의 경우가 hidden state를 추정하기 위함이라고 볼 수 있다.
측정값과 모델이 Correlation 관계에 있는 칼만 시스템 분산 이동 과정을 X는 종방향 위치, $\dot X$는 종방향 속도이고, 측정값은 종방향 위치(X)인 아래 예시로 살펴보자.

모델 equation:
${X_{k+1} = X_k + dt* \dot X_k }$
아웃풋 equation:
$Y_{k+1} = X_{k+1}$

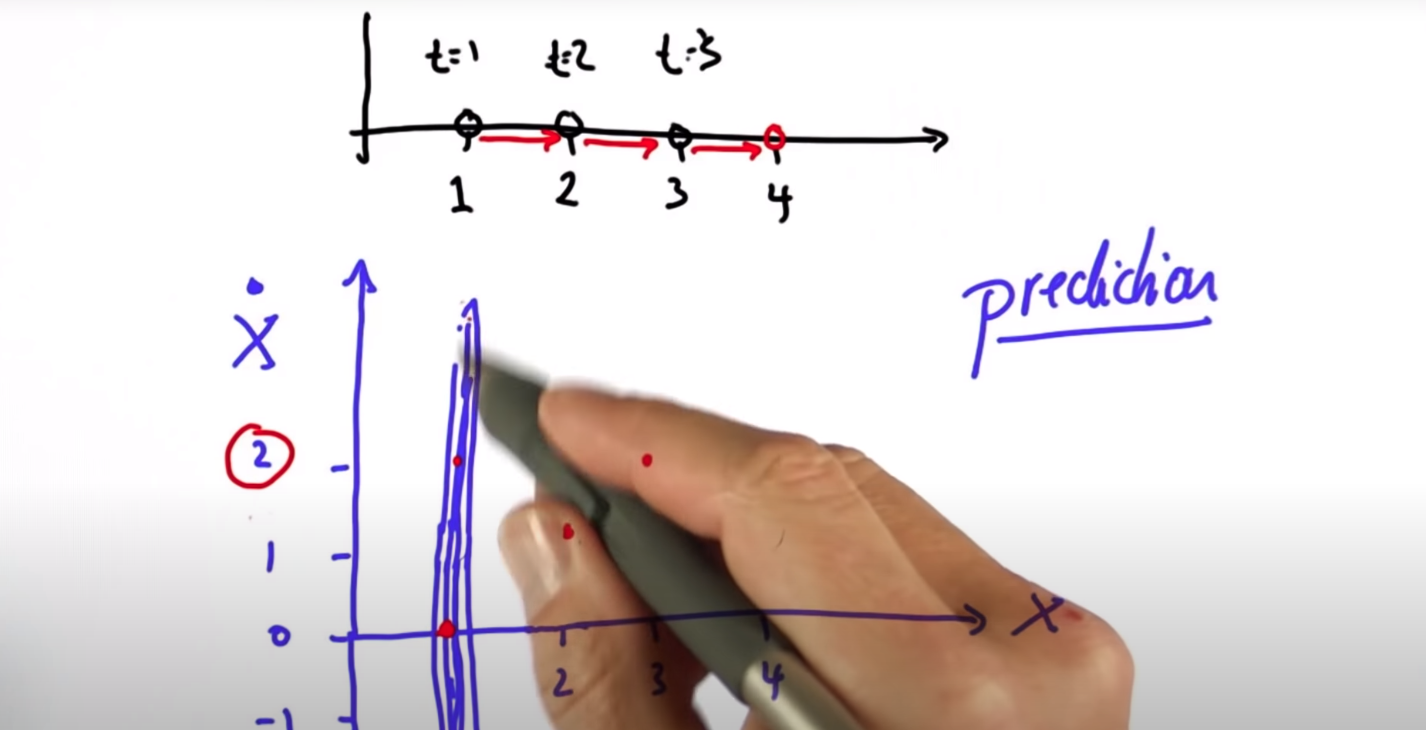
X 초기값이(t=1) 1로 주어졌다. 이 상태에서 속도 값은 관측되지 않으므로 알 수 없으므로 속도 방향으로는 큰 분산을 갖는다.(파란색 분포)

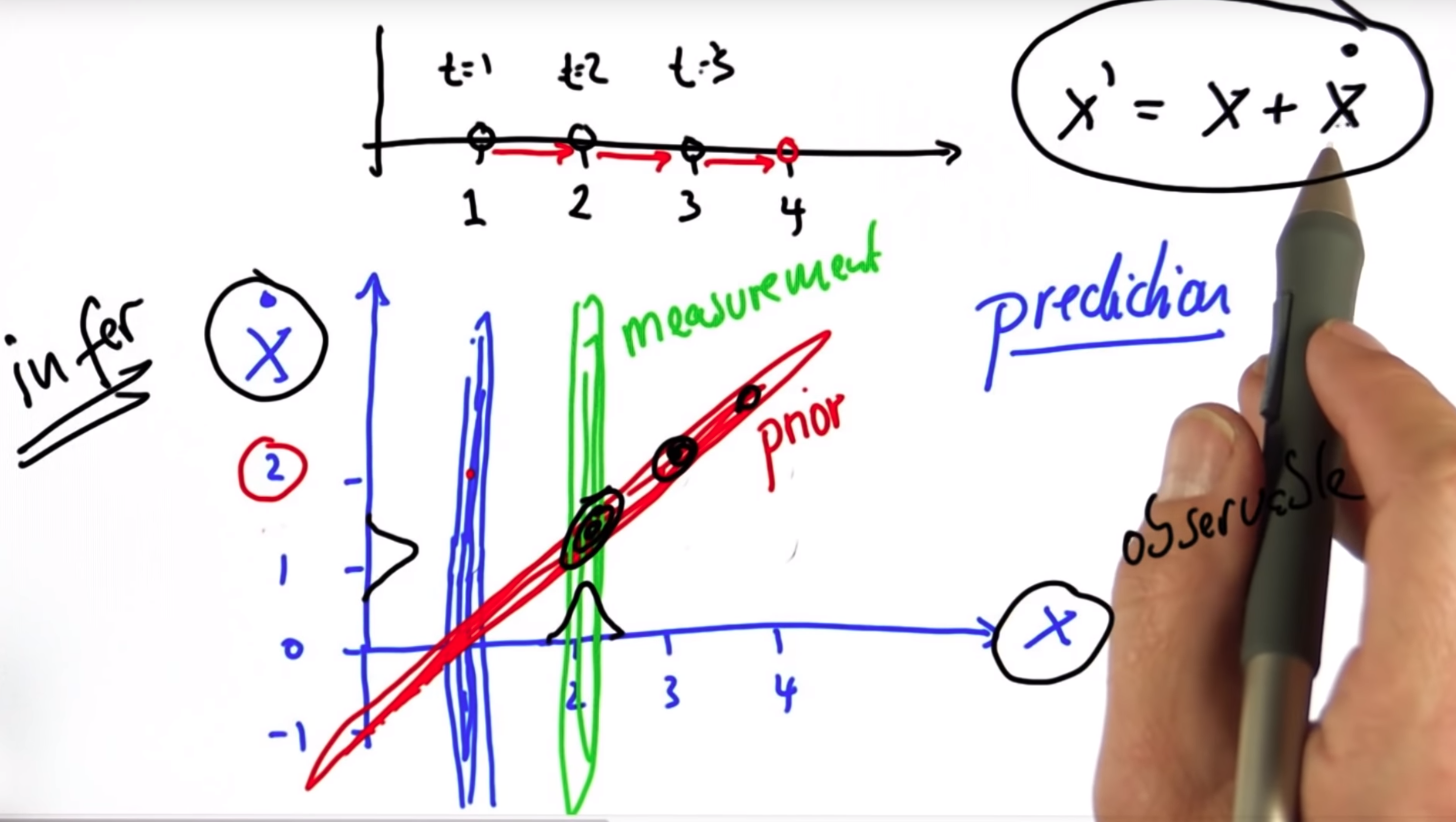
(t=2) 일때, 위치가 2로 관측되었다(Measure, 초록색 분포). 여기서 모델에 의해 $\dot X_k$ 속도는 1로 계산이 되어, 모델 예측값이 생기게 된다(Prior, 빨간색 분포). 측정된 위치정보 뿐 아니라, 모델 예측 정보도 이용할 수 있게 된 것이다. Measure와 Prior의 보정 Update 과정을 통해 칼만 시스템의 분산(P, 검은색 분포)이 계산되고, 이 과정을 반복함에 따라 칼만 필터는 물체의 위치를 잘 추정하게 된다. (P, 검은색 분포가 점점 수렴함)

그림을 다시한번 보자. 모델에선 빨간색 모양으로 1차 함수 형태의 Prior 분산이 생기고, 측정값에선 위치만 계측하고 있으니 초록색 모양으로 수직의 Measure 분산을 갖게 된다. 칼만필터는 이 둘의 교차점에서 보정되는 새로운 분산을 계산해냄으로써 추정 결과를 보정하는 것이다. 모델과 측정값의 correlation 관계를 이용하여 보정이 된다. 그리고 시간이 흐름에 따라 보정 결과는 더욱 더 정확해지게 된다.
insight를 주는 부분이라고 생각한다. Udacity Lecture를 참고하여 학습하는 것을 추천한다.
다차원 칼만필터는 아래와 같이 수식 정리가 된다. 아래의 수식은 정리된 최종 수식이다.
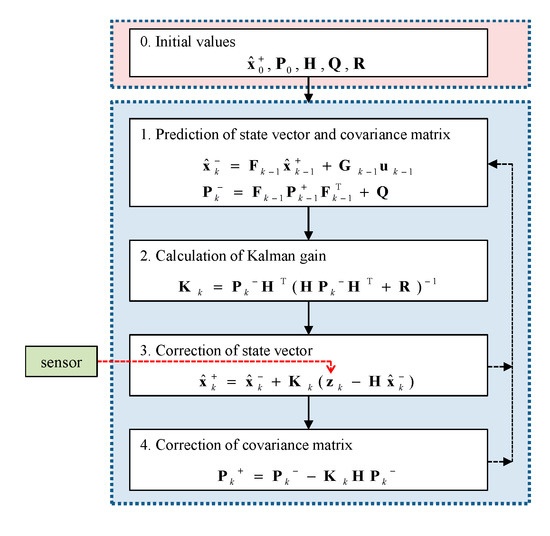
Eigen 라이브러리를 이용하여 칼만필터 구현

아래 구현 문제:
종방향 위치, 속도를 상태변수로 하는 로봇 시스템을 생각해보자. input은 시스템에 가해지는 가속도이고, 계측되는 정보는 위치 정보이다. 해당 로봇 시스템의 위치와 속도를 추정하는 필터를 설계하자.

#include <iostream>
#include "Eigen/Dense"

class Kalman{
    public:
    Kalman(int size, double sampling_time, Eigen::MatrixXd& _Ac, Eigen::MatrixXd& _Bc, Eigen::MatrixXd& _Cc, Eigen::MatrixXd& _P, Eigen::MatrixXd& _Q, Eigen::MatrixXd& _R){
        state_size = size;
        dt = sampling_time;

        Ad = _Ac * dt + Eigen::MatrixXd::Identity(size, size);
        Bd = _Bc * dt;
        Cd = _Cc;

        P = _P;
        Q = _Q;
        R = _R;

        state = Eigen::MatrixXd::Zero(size,1);
    }

    void model_prediction(double input){

        state = Ad*state + Bd*input;
        P = Ad*P*Ad.transpose() + Q;
        
        std::cout << "* predict: \n";
        std::cout << "state(position , velocity) is \n";
        std::cout << state << std::endl;
        std::cout << "kalman covariance is \n";
        std::cout << P << std::endl << std::endl;        

    }
    void measure_update(double measure){

        Eigen::MatrixXd meas(1,1);
        meas << measure;
        
        K = P*Cd.transpose()* (Cd*P*Cd.transpose() + R).inverse();
        state = state + K* ( meas - Cd*state);
        P = P - K*Cd*P;

        std::cout << "** update: \n";
        std::cout << "state(position , velocity) is \n";
        std::cout << state << std::endl;
        std::cout << "kalman covariance is \n";
        std::cout << P << std::endl << std::endl;
    }

    private:
    Eigen::MatrixXd state;
    Eigen::MatrixXd Ad;
    Eigen::MatrixXd Bd;
    Eigen::MatrixXd Cd;
    
    double dt;
    int state_size;

    Eigen::MatrixXd P, Q, R;
    Eigen::MatrixXd K;
};

int main(){

    // 칼만 시스템 매트릭스 및 분산값 세팅
    int size = 2;
    Eigen::MatrixXd Ac(size,size);
    Ac << 0,1,0,0;
    Eigen::MatrixXd Bc(size,1);
    Bc << 0,1;
    Eigen::MatrixXd Cc(1,size);
    Cc << 1,0;

    Eigen::MatrixXd P(2,2);
    Eigen::MatrixXd Q(2,2);
    Eigen::MatrixXd R(1,1);
    P = Eigen::MatrixXd::Identity(size,size) * 1000;
    Q = Eigen::MatrixXd::Identity(size,size) * 0;
    R << 1;

    // 칼만 필터 RUN
    Kalman kf(2, 1, Ac, Bc, Cc, P, Q, R);
    std::vector<double> inputs = {2,0,0,0};
    std::vector<double> measures = {1,3,5};
    for (int i = 0 ; i < measures.size() ; ++i){
        std::cout << "=======> Iter: " << i+1 << std::endl;
        kf.model_prediction(inputs[i]);
        kf.measure_update(measures[i]);
    }
    std::cout << "=======> Predict: "  << std::endl;
    kf.model_prediction(inputs.back());

    return 0;
}

4. Conclusion

Extended Kalman도 비선형 모델을 선형화해서 접근하는 것으로 분산 값의 이동과 모델 state의 이동을 perturbation linearization으로 선형화하여 linear kalman 필터와 동일한 방식으로 접근한 것이다. dt가 작고, 비선형성이 크지 않다면 선형화하여 풀어도 좋은 성능을 보인다.

Kalman Filter- Essential

칼만필터에 대한 학습, equation 유도, c++ 구현

2021-09-12 10:10