Algorithm: Program Solving(c++)

작성자: SungwookLE
작성일: ‘22.3/14

1. 본 페이지에서는 무엇을 배우나요?

1-1. 문제해결, Program Solving(PS)을 위한 알고리즘 설계 문제를 배웁니다.

• 다른 말로, 코딩테스트 문제라고 불러요 😢

  알고리즘 공부, 어떻게 해야하나요?

• 본 페이지는 아래 강의를 따라가며 작성하였어요.

  IT 기업 취업을 위한: 코딩 테스트 혼자서 정복하기

1-2. 데이터베이스나 복잡한 구조에서 효율적인 알고리즘(Big O) 설계를 위한 방법을 배웁니다.

• 시각복잡도Big O 에 대해 알아봐요 👊

  개발자라면 이제는 알아야하는 Big O 설명해드림. 10분컷.

1-3. 효율적인 알고리즘 만큼 중요한 것은 Clean Code 작성이라는 사실!

• Variable, Function, Class 의 이름만 잘 지어도 Clean Code가 될 수 있어요. 💯

  깨끗한 코드를 위한 5가지 팁

2. 시간복잡도(BigO) 먼저 짚고 시작해요

• 알고리즘의 효율성의 가장 기본적인 비교 메트릭은 BigO 방법이예요.

`BigO`는 인풋 사이즈(`N`)에 대한 함수의 실행횟수를 말합니다.

• 다음의 대표적인 방식에 대한 BigO를 계산해보면,
  1. 인풋 배열(사이즈N)에서 하나의 값을 바로 출력: O(1)
  2. 인풋 배열(사이즈N)을 1중 for문으로 조회: O(N)
  3. 인풋 배열(사이즈N)을 2중 for문(nested loop)으로 조회: O(N^2)
  4. 인풋 배열(사이즈N)을 n중 for문(nested loop)으로 조회: O(N^n)
  5. 인풋 배열(사이즈N)을 Binary Search 알고리즘으로 특정 값을 출력: O(logN)

     • Binary Search 알고리즘은 인풋 배열을 매 스텝마다 반으로 잘라 왼쪽과 오른쪽으로 쪼개나가며 특정 값을 찾아나가는 특징이 있는 알고리즘이예요.

         void binary_search(input_array){
         	if (특정값 찾기 성공)
         		return answer;
           else{
         	  left_side = input_array[0:mid]
         		right_side = input_array[mid:-1]
         	  binary_sarch()
         	}
         }
       

       • Binary Search 알고리즘의 BigO 실행횟수(step)는 logN 이 됩니다.
       • BigO 표기법에서는 log의 밑 2를 표기하지 않고 생략하니 참고하세요.

       • Binary Search 알고리즘을 사용하여, 32개의 인풋사이즈를 갖는 배열의 특정 값을 찾는 경우를 생각해봅시다.

           32개의 인풋 배열이 입력되면,
                         
           32 / 2 = 16 <- 1 step
           16 / 2 = 8  <- 2 step
           8  / 2 = 4  <- 3 step
           4  / 2 = 2  <- 4 step
           2  / 2 = 1  <- 5 step
                         
           특정값을 찾는 worst case를 가정하고 살펴보아도
           최대 실행횟수는 logN = 5 가 되네요.
         

• 공간복잡도에 대해서도 알아두면 좋아요. (메모리 관점)
  • BigO 표현법 기준으로 배열의 최대 사이즈가 공간복잡도입니다.
  • 프로그램의 소요시간 뿐만 아니라, 사용되는 메모리도 중요합니다. 여러분들의 컴퓨터의 메모리는 한정되어 있기 때문에, 똑같은 프로그램이면 차지하는 메모리가 적은게 더 좋겠죠? 그렇기 때문에 시간복잡도 뿐만 아니라 공간복잡도도 중요합니다.
  • 보통 메모리를 계산하는 경우에는 C++을 기준으로 생각합니다. C++ 에서는 int가 4 byte, char이 1 byte, double이 8 byte, short가 2 byte 이렇게 정해져 있습니다.

  • int로 2천만이 대략 80 MB라는 것을 이용하여 다음과 같이 쉽게 계산이 가능합니다.

      int a[2천만] : 80MB
      int a[2백만] : 80 / 10 = 8MB
      char a[2천만] : 80 / 4 = 20MB
      double a[2천만] : 80 * 2 = 160MB
    

  • int 1개(4byte) x 2천만 = 80,000,000 = 80*10^6 = 80 MB

  • 예제를 살펴봅시다.

      function solution(n)
      	set list = [n][n][n]
      	for i= 0 ... i < n
      		set tmp = [n]
      		for j = 0 ... j < n
      			tmp[j] = list[0][i][j]
    

    • 정답: 공간복잡도는 배열 최대 크기인 O(N^3) 이고, 참고로 시간복잡도는 O(N^2)

3. PS Dynamic Programming 동적 프로그래밍

• Dynamic Programming = 분할정복 프로그래밍 = 점화식 배열
• 분할정복 풀이: Bottom-up 방식으로 점화식(recurrence relation)을 유도하여 풀자
  • 문제를 직접 풀려고 if문을 생각하게 되면, 여러 예외조건에 막혀 문제를 풀 수 없게된다는 것을 명심
  • 분할정복 문제는 배열을 이용해서 풀게되는데, 이 때!, 0 번째 케이스에 대한 값을 {공집합, 0}과 같은 default 값을 넣어줌으로써 trivial case 에 대한 값을 명시적으로 배열을 채워서 풀자.
  • Top-down 방식으로 풀어야하는 문제도 있으나, 대부분 Bottom-up 방식이 풀기 쉽다.

3.1. 컨셉

1. 수열의 n번째 값 a_n을 구하기 위해 따라야 하는 규칙
2. a_n을 구하기 위해서는, a_1부터 순서대로 계산해야 함
   • Bottom-up 방식으로 동적 프로그래밍을 위한 점화식 배열 문제 풀기

   • 배열을 이용한 점화식 풀이 방법

     

   • 실제 코딩테스트 문제는 점화식을 주지 않으니, 직접 유도해야 한다.

    int main(){
    	int n ; 
    	cin >> n;
           
    	vector<int> arr = {3};
    	//bottom-up 방식
    	for(int i = 1  ; i <= n ; ++i)
    		arr.push_back(arr[i-1]*2 -4);
           
    	cout << arr[n] << endl;
    	return 0;
    }
   

3-2. 개념문제(1차원)

큰 문제를 작은 문제부터 해결하여 계산하기: 1차원 배열

• 특정 금액을 만들 수 있는 동전의 최소 개수를 찾아라

  

  1. 풀이: 20원으로 조합되기 위한 조합의 수는 15원의 조합+1 또는 17원의 조합+1 의 조합의 수를 갖는다.

     

  2. 점화식(recurrent function):

     

  3. DP 배열 설계:

     

  4. 코드:

      int main(){
             
          int N;
          cin >> N;
             
          vector<int> DP(N+1, 0);
             
          //bottom - up
          // 1) 초항
          DP[0] = 0;
          DP[1] = X;
          DP[2] = X;
          DP[3] = 1;
          DP[4] = X;
          DP[5] = 1;
             
          // 2) 점화식
          // DP[6] = min(DP[6-3]+1 , DP[6-5]+1);
          //        = min(DP[3]+1, DP[1]+1);
          //        = min(DP[3]+1)
             
          for(int i = 6 ; i <= N ; ++i){
             
              if (DP[i-3] == X){
                  if (DP[i-5] == X)
                      DP[i] = X;
                  else if (DP[i-5] != X)
                      DP[i] = DP[i-5]+1;
              }
              else if (DP[i-3] != X){
                  if (DP[i-5] == X)
                      DP[i] = DP[i-3]+1;
                  else if (DP[i-5] != X)
                      DP[i] = min(DP[i-3]+1, DP[i-5]+1);
              }
          }
          cout << DP[N] << endl;
             
          return 0;
      }
     

3-3. 연습문제(2차원)

큰 문제를 작은 문제부터 해결하여 계산하기: 2차원 배열

• 가방에 담을 수 있는 보석의 최대 값어치를 담아서 훔쳐라

  

  1. 풀이: 작은 문제들을 풀어나가는 과정을 통해 N=4, K=14라고 하였을 때의 최대 값어치를 찾아보는 것을 생각해보자.

     

  2. 점화식:

      if (j >= W)
          DP[i][j] = max(DP[i-1][j], DP[i-1][j-W]+current_price)
       // 배낭의 무게 허용량(j)이 보석의 무게(W)보다 크다면, 새로운 보석을 넣었을 때와 넣지 않았을 때의 max값이 가방에 들어갈 수 있는 보석의 최대값어치이다. 
      else if (j < W)
          DP[i][j] = DP[i-1][j]
      // 보석의 무게(W)가 배낭 허용량(j)보다 무거운 케이스
     

  3. 코드

      int main(){
             
          int N, K;
          cin >> N >> K;
             
          vector<vector<int>>DP(N+1, vector<int>(K+1,0));
             
          for(int i = 1 ; i <= N ; ++i){
             
              int W, P;
              cin >> W >> P;
             
              for(int j = 1; j <= K; ++j){
                  if ( j >= W )
                      DP[i][j] = max(DP[i-1][j] , DP[i-1][j-W] + P);
                  else if ( j < W)
                      DP[i][j] = DP[i-1][j];
              }
          }
             
          cout << DP[N][K] << endl;
          return 0;
      }
     

• 주어진 두개의 문자열의 LCS(Longest Common Sequence)를 찾아라

  

  1. 풀이: 작은 문제들을 풀어나가는 과정을 통해 LCS를 찾아내자.
  2. 문제의 조건에서 LCS는 연속적일 문자열일 필요는 없었다.

  3. 점화식:

     

      vector<vector<int>> DP(A.length()+1, vector<int>(B.length()+1,0));
          string A_token_last;
          for(int i = 1 ; i <= A.length(); ++i){
              A_token_last = A[i-1];
              string B_token_last;
              for(int j = 1 ; j <= B.length(); ++j){
                  B_token_last = B[j-1];
                  if (A_token_last == B_token_last)
                      DP[i][j] = DP[i-1][j-1]+1; 
          //두 문자열의 마지막 문자가 같다면, LCS("A문자열에서 마지막 문자 제거", "B문자열에서 마지막 문자 제거") + 1 의 값의 DP[i][j]의 LCS 최대값
                  else
                      DP[i][j] = max(DP[i-1][j], DP[i][j-1]);
          //두 문자열의 마지막 문자가 다르다면, max(LCS("A문자열", "B문자열에서 마지막 문자 제거"), LCS("A문자열에서 마지막 문자 제거", "B문자열"))
              }
          }
     

  4. 코드

      int main(){
          string A, B;
          cin >> A >> B;
             
          vector<vector<int>> DP(A.length()+1, vector<int>(B.length()+1,0));
          string A_token_last;
          for(int i = 1 ; i <= A.length(); ++i){
              A_token_last = A[i-1];
              string B_token_last;
              for(int j = 1 ; j <= B.length(); ++j){
                  B_token_last = B[j-1];
             
                  if (A_token_last == B_token_last)
                      DP[i][j] = DP[i-1][j-1]+1;
                  else
                      DP[i][j] = max(DP[i-1][j], DP[i][j-1]);
              }
          }
             
          for(auto elements : DP){
              for(auto element : elements)
                  cout << element << " ";
              cout << endl;
          }
             
          cout << "ANSWER: " << DP[A.length()][B.length()] << endl;
             
          return 0;
      }
     

• 프로그래머스 문제: 최소 N을 사용하여 주어진 number를 만드는 개수를 찾아라
  • 문제: N으로표현

  • 문제 설명:

      아래와 같이 5와 사칙연산만으로 12를 표현할 수 있습니다.
      12 = 5 + 5 + (5 / 5) + (5 / 5)
      12 = 55 / 5 + 5 / 5
      12 = (55 + 5) / 5
            
      5를 사용한 횟수는 각각 6,5,4 입니다. 그리고 이중 가장 작은 경우는 4입니다.
      이처럼 숫자 N과 number가 주어질 때, N과 사칙연산만 사용해서 표현 할 수 있는 방법 중 N 사용횟수의 최솟값을 return 하도록 solution 함수를 작성하세요.
            
      * 제한사항
      N은 1 이상 9 이하입니다.
      number는 1 이상 32,000 이하입니다.
      수식에는 괄호와 사칙연산만 가능하며 나누기 연산에서 나머지는 무시합니다.
      최솟값이 8보다 크면 -1을 return 합니다.
    

  1. 문제 풀이: bottom-up으로 풀 수 있는 배열을 설계하여 풀자(점화식)

     

  2. 코드:

      #define max_K 8
      using namespace std;
             
      int get_Ns(int N, int idx){
          int Ns=N;
          for(int i = 1 ; i < idx ; ++i){
              Ns = Ns*10 + Ns;
          }
          return Ns;
      }
             
      int main(){
          int N, number;
          cin >> N >> number;
          vector<unordered_set<int>> DP(max_K+1);
          DP[0].insert(0); //trivial case
          for(int k = 1; k <= max_K; ++k){
              DP[k].insert(get_Ns(N, k));
                 
              for(int i = 1 ; i <= k; ++i){
                  for(int j = 1;  j<= k ; ++j){
                      if ((i+j) != k)
                          continue;
             
                      for(int p : DP[i]){
                          for(int q: DP[j]){
                              DP[k].insert(p+q);
                              DP[k].insert(p*q);
             
                              if ( p - q > 0)
                                  DP[k].insert(p-q);
                              if ( p / q > 0 )
                                  DP[k].insert(p/q);
                          }
                      }
                  }
              }
             
              if( DP[k].find(number) != DP[k].end()){
                  cout << "Find: " << *(DP[k].find(number)) << endl; // 
                  cout << "ANSWER: " << k << endl;
                  return k;
              }
          }
          cout << "ANSWER: " << -1 << endl;
          return -1;
      }
     

• 프로그래머스 문제: 삼각형의 최대 합을 찾아라
  • 문제: 정수삼각형

  • 문제 설명:

    

    • 위와 같은 삼각형의 꼭대기에서 바닥까지 이어지는 경로 중, 거쳐간 숫자의 합이 가장 큰 경우를 찾아보려고 합니다. 아래 칸으로 이동할 때는 대각선 방향으로 한 칸 오른쪽 또는 왼쪽으로만 이동 가능합니다. 예를 들어 3에서는 그 아래칸의 8 또는 1로만 이동이 가능합니다.삼각형의 정보가 담긴 배열 triangle이 매개변수로 주어질 때, 거쳐간 숫자의 최댓값을 return 하도록 solution 함수를 완성하세요.
    • 제한사항삼각형의 높이는 1 이상 500 이하입니다.삼각형을 이루고 있는 숫자는 0 이상 9,999 이하의 정수입니다 1. 문제 풀이: bottom-up으로 풀 수 있는 배열을 설계하여 풀자(점화식 )
    • 처음 생각한 방식은 삼각형의 위에서 부터 모든 경로에 대한 경우의 수를 따지는 것은 동적프로그래밍이라기 보다는 브루트포스 방식(모든 경우를 naive하게 전부 계산)가 된다.

    • 삼각형의 밑변에서 부터 시작하여 최대 합이 나오는 것을 선택해주면 모든 경우의 수를 따지지 않고서 삼각형 경로의 최대합을 구할 수 있다.

        DP[i][j] = max( DP[i-1][j] + triangle[height-i][j-1],DP[i-1][j+1] + triangle[height-i][j-1]);
      

      

  1. 코드:

      int main(){
             
          // triangle 값 입력받기
          int height;
          cin >> height;
          vector<vector<int>> triangle(height);
          int element;
          for(int i = 1 ; i <= height ; ++i){
              for (int j = 1 ; j <= i ; ++j){
                  cin >> element;
                  triangle[i-1].push_back(element);
              }
          }
             
          //solution
          cout << endl;
          cout << "DP array below: "<< endl;
          vector<vector<int>> DP(height+1, vector<int>(height+2,0));
          for(int i = 1; i <= height; ++i){
              for(int j = 1; j <= height - (i-1); ++j){
             
                  DP[i][j] = max( DP[i-1][j] + triangle[height-i][j-1],
                                  DP[i-1][j+1] + triangle[height-i][j-1]);
             
                  cout << DP[i][j] << " ";
              }
              cout << endl;
          }
             
          cout << endl << "ANSWER: " << DP[height][1] << endl;
          return 0;    
      }
     

4. PS 그래프 탐색 BFS, DFS

• 그래프(Graph)는 노드(상태)와 엣지로 이루어져 있음
• 그래프 탐색 알고리즘은 BFS(너비우선탐색)와 DFS(깊이우선탐색) 알고리즘으로 나뉜다.
  1. BFS(Breadth First Search, 너비우선탐색)
     • 탐색 후, 노드 방문
     • 큐(queue)를 사용하여 문제 해결
     • 큐(queue)는 Last In Last Out의 데이터 배열 자료구조를 말해요
     • 큐(queue)의 역할은 탐색한 노드(방문 예정 노드)를 저장하는 역할을 합니다.
  2. DFS(Depth First Search, 깊이우선탐색)
     • 즉시 노드를 방문 (탐색 X)
     • 스택(stack)을 사용하여 문제 해결
     • 스택(stack)은 Last In First Out의 데이터 배열 자료구조를 말해요
     • 스택(stack)의 역할은 지금까지 방문한 노드를 모두 저장하는 역할을 합니다. (Trace)

4-1. BFS, DFS 컨셉 및 개념문제

1. 다리로 이어져 있는 군도에서 목표 섬에 가는 경로를 찾아라
   • 문제 설명
     • 지웅이는 A 위치에서 목적지인 F까지 이동하고 싶다. (시작점 A, 목적지 F)

     

     • BFS를 이용한 풀이: 가까이 있는 섬부터 탐색하기 (너비우선탐색)
       • 큐(queue)를 사용하여 BFS문제를 풀어요.
       • 큐에 있는 노드는 탐색하여 갈 수 있는 노드이지만, 방문은 하지 않은 노드예요. 즉, 갈 수 있는 노드 후보지(candidates)를 큐에 담아두었어요. 큐에서 꺼낼 때(pop) 해당 노드를 방문할거예요.
         1. default 상태 (어느 섬에도 있지 않음)

         

       1. A섬에서 방문하고 탐색을 시작(큐에서 첫번째인 A를 꺼냄)

          

          • B와 C노드가 탐색되어 큐에 넣어줌(갈 수 있는 후보지)

       2. B섬에 방문하고 탐색을 시작(큐에서 첫번째인 B를 꺼냄)

          

          • D노드가 탐색되어 큐에 넣어줌(갈 수 있는 후보지)

       3. C섬에 방문하고 탐색을 시작(큐에서 첫번째인 C를 꺼냄)

          

       4. D섬에 방문하고 탐색을 시작(큐에서 첫번째인 D를 꺼냄)

          

          • D섬에서는 갈 수 있는 섬이 없으니 추가할 후보지 노드는 없네요.

       5. F섬에 방문하고 탐색을 시작(큐에서 첫번째인 F를 꺼냄)

          

          • F섬은 목적지였으니, 탐색을 종료한다. 경로의 길이는 2이다.

          

          • 최종 경로는 A - C - F 의 순서로 2번만에 목적지 섬으로 이동 가능하다. (최단 경로)
     • DFS를 이용한 풀이: 최대한 깊숙한 곳까지 탐색하기 (깊이우선탐색)
       • 스택을 이용하여 문제를 풀어요
       • 스택에 담겨져 있다는 것은 해당 섬을 방문했다는 의미예요
         1. A섬에서 시작 (A섬에 방문한 상태)
         • 스택에 담는다.

         

       1. B섬에 방문

          

       2. D섬에 방문

          

          • 더 이상 나아갈 곳이 없다. (깊이의 끝에 도달)
          • D섬을 스택에서 지우고(pop) 이 전 지점인 B로 돌아가자

       3. B섬에 돌아와서 C섬에 방문

          

          • 이 부분에서 DFS와 BFS의 차이점이 보이는데, C섬으로 오는 경로에 있어서 DFS는 A-B-C 의 경로로 이동하였지만, BFS의 경우에는 A-C의 경로로 올 수 있었다.

       4. F섬에 방문

          

          • 목적지인 F섬에 도달하였으니 DFS 탐색을 멈춘다.

          • 지웅이의 이동 경로는 스택의 순서대로, A-B-C-F가 된다.

            

          • DFS 알고리즘을 통해 경로를 찾는 경우, 최단 경우를 알려주는 것은 아닐 수도 있다.
          • 그러나, 경우에 따라서 DFS 로만 풀어야지 풀 수 있는 문제가 있다.
2. 2차원 격자 속 미로 탈출
   • 문제 설명
     • 민영이는 S(1,1)에서 E(4,3)로 가고 싶다.

     

     • BFS를 이용한 미로찾기 경로탐색 (너비우선탐색)
       • 큐에서 원소 제거(pop): 좌표 방문
       • 큐에서 원소 삽입(push): 탐색한 좌표를 방문 후보지에 추가
         1. 시작지점(1,1)에서 시작

         

       1. (1,2) 방문
          • 추가할 수 있는 탐색한 방문 후보지가 없음 (큐에 추가 X)
       2. (2,1) 방문
          • 탐색: (3,1) 추가 가능

          

       3. (3,1) 방문
          • 탐색: (3,2) 추가 가능

          

       4. (3,2) 방문
          • 탐색: (3,3), (4,4), (2,2) 추가 가능

          

       5. (3,3) 방문

          

          • 후보지를 탐색하니 목표로 하는 도착지점 (4,3)이 탐색됨

          

       6. 큐에 있는 나머지 노드를 방문하고 탐색 수행하고 (4,2), (2,2) …
       7. (4,3) 방문
          • 도착지점에 도달하였으니, BFS 탐색 종료

          • (1,1)부터 (4,3)까지 5번의 이동으로 최단 경로를 찾아냄

            

     • DFS를 이용한 미로찾기 경로탐색 (깊이우선탐색)
       • 스택 원소 삽입(push): 새로운 좌표 방문
       • 스택 원소 제거(pop): 이전 위치로 복귀
         1. 시작지점(1,1)에서 시작

         

       1. (1,2)에 방문

          

          • 더 이상 갈 곳이 없으니까, 이전 위치로 pop (깊이의 끝)

       2. (2,1)에 방문

          

       3. (3,1)에 방문

          

       4. (3,2)에 방문

          

          • (3,2)에서 3방향으로 이동 가능하나, 위부터 방문한다고 치면 (3,3)부터 방문
          • 어느 방향부터 방문할지는 임의대로 규칙을 정해 따르면 됨

       5. (3,3)에 방문

          

       6. (4,3)에 방문

          

          • 목적지인 (4,3)에 도착하여 DFS 탐색 종료
          • 이동한 경로는 스택에 담겨져 있는 순서로 5번의 이동 경로 발생
            • (BFS와 동일한 최단 거리를 찾아냄)

4-2. BFS 연습문제

• BFS(Breadth First Search, 너비우선탐색)
  • 탐색 후, 노드 방문
  • 큐(queue)를 사용하여 문제 해결
  • 큐(queue)는 Last In Last Out의 데이터 배열 자료구조를 말해요
  • 큐(queue)의 역할은 탐색한 노드(방문 예정 노드)를 저장하는 역할을 합니다.
• 큐(방문 가능한 노드 리스트)에 추가가 되지 않는 조건
  1. 그래프나 그리드를 벗어나는 탐색 공간
     • if ((next.x >= 시작 && next.y >= 시작) && (next.x <= 끝 && next.y <= 끝)
  2. 방문한 곳은 또 방문하지 않는다. 비효율 경로를 발생시키기 때문
     • if (grid[next.x][next.y] == 방문 안한 곳)
• 장기판에서 말을 원하는 곳으로 옮기는 데 필요한 최소 회수를 구해라

  • 문제 설명:

    

  • 문제 풀이:

    1. 초기값: 큐에 이동 가능한 좌표(시작 좌표)를 넣는다.

       

    2. 시작좌표에 방문하고, 이동 가능한 탐색한 공간을 큐에 넣는다.

       • 시작좌표 노드를 pop하여 꺼냄

         

       • 방문 가능한 탐색한 공간을 큐에 넣는다.

         

       • 총 8개의 공간이 이동 가능한 좌표로 큐에 추가된다.

         

    3. 큐의 첫번째인 (6,5)부터 방문하여 탐색한다.
       • (6,5)를 pop 하여 꺼내기

       • 탐색 공간을 찾고 큐에 넣어주기

         

       • 이 때 큐에 목표지점인 (4,6)이 들어와 있음을 볼 수 있다.
    4. 큐의 첫번째인 (6,3) 부터 방문하여 탐색과정을 반복하여 진행
    5. (어느 순간) 큐의 첫번째인 목표지점(4,6)에 방문
       • 목표지점(4,6)에 도착하여 BFS탐색 종료

    • 코드 구현

        #include <iostream>
        #include <queue>
        #include <vector>
        using namespace std;
                  
        //1. 문제의 조건을 입력받는 변수나 배열은 글로벌 변수로 선언해주는 것이 편리하다.
        //2. 배열같은 경우, 딱 맞게 사이즈를 선언하는 것 보다는 문제 조건에서 최대 조건을 따져서 크게 잡아주는 것이,
        //   유리한데, 문제를 푸는 데 있어서 불필요하게 발생할 수 있는 메모리 에러를 피할 수 있다.
                  
        int N, M;
        int sx, sy, fx, fy;
        vector<vector<int>> grid(110, vector<int>(110,0));
        queue<pair<int, int>> q;
        vector<pair<int, int>> delta = { {2,1}, {2, -1}, {-2,1}, {-2, -1},
                                         {1,2}, {1, -2}, {-1,2}, {-1, -2} };
                  
        int main(){
                  
            cin >> N >> M;
            cin >> sx >> sy;
            cin >> fx >> fy;
            q.push({sx, sy});
                  
            //---------------- |solution| ----------------
            while(q.size() > 0){
                  
                pair<int, int> now = q.front(); // peek
                q.pop();
                  
                cout << "NOW:{" << now.first << "," << now.second 
                << "}, COUNT:" << grid[now.first][now.second] << endl;
                          
                if (now.first == fx && now.second == fy){
                    cout << "FIND(BFS): " << grid[fx][fy] << endl;
                    return 0;
                }
                  
                for (auto d_move : delta){
                    pair<int, int> next = {now.first+d_move.first , now.second+d_move.second}; 
                              
                    if ((next.first >= 1 && next.second >=1) && (next.first <= N && next.second <= M) && // 장기판 안에서만 움직여야 하고
                        (grid[next.first][next.second] == 0) ){  // 방문하지 않은 곳만 추가한다.
                            q.push(next);
                            grid[next.first][next.second] = grid[now.first][now.second]+1;
                        }
                }
            }    
                  
            cout << "NO PATH" << endl;
            return 0;
        }
      

• 박스 안에 귤이 모두 상하는 데 걸리는 최소 날짜는 얼마일까

  • 문제 설명:

    

  • 문제 풀이:

    1. 시작 값(상한 귤의 좌표)를 큐에 넣어 준다.

       

       • 상한 귤은 1, 상하지 않은 귤은 0, 비어 있는 공간은 X(-1)로 표시하였다.

    2. 큐 제일 앞에 있는 (1,2)를 꺼내 방문하고, 이 지점을 기준으로 주변의 상하게 될 귤을 큐에 추가한다.

       

       • 상하게 될 귤의 그리드 값은 +1을 해주어 표시한다. (모든 귤이 상하는 데 걸리는 날짜 표시)

    3. 큐 제일 앞에 있는 (3,1)을 꺼내고, 주변의 상하게 될 귤을 큐에 추가한다.

       

    4. 큐 제일 앞에 있는 (4,3)을 꺼내고, 주변의 상하게 될 귤을 큐에 추가한다.

       

    5. 큐 제일 앞에 있는 (1,3)을 꺼내고, 주변의 상하게 될 귤을 큐에 추가한다.
    6. 큐가 모두 비워질 때 까지 반복한다. (도달할 수 있는 경로 X)
    7. 큐가 모두 비워져 있다면, 큐를 순회하며 최대값을 리턴한다.
       • 리턴되는 값의 -1을 한 것이 귤이 전부 상하게 될 때까지 걸리는 날짜이다.
       • 순회 중에 0의 값이 발견된다면, 모든 귤이 상하지 않았단 의미이므로 문제의 조건대로 -1을 리턴해요.

    • 코드 구현:

        #include <iostream>
        #include <vector>
        #include <queue>
        using namespace std;
                  
        int N, M;
        vector<vector<int>> grid_orange_box(1010, vector<int>(1010,0));
        vector<pair<int, int>> delta = { {-1,0},{1,0},{0,-1},{0,1} };
        queue<pair<int, int>> queue_weird_oranges;
                  
        int main(){
                  
            cin >> N >> M;
            for(int i = 1 ; i <= N ; ++i){
                for(int j = 1 ; j <= M ; ++j){
                    cin >> grid_orange_box[i][j];
                  
                    if (grid_orange_box[i][j] == 1)
                        queue_weird_oranges.push({i,j});
                }
            }
                      
            // ------ |solution| ------ 
            while(!queue_weird_oranges.empty()){
                pair<int, int> now = queue_weird_oranges.front();
                queue_weird_oranges.pop();
                  
                cout << "NOW:{" << now.first << "," << now.second 
                << "}, COUNT:" << grid_orange_box[now.first][now.second] << endl;
                  
                for(auto d : delta){
                    pair<int, int> next = {now.first + d.first , now.second + d.second};
                    if (next.first >= 1 && next.second >= 1 && next.first <= N && next.second <= M){
                                  
                        if (grid_orange_box[next.first][next.second] == -1)
                            continue;
                  
                        if (grid_orange_box[next.first][next.second] == 0){
                            queue_weird_oranges.push(next);
                            grid_orange_box[next.first][next.second] = grid_orange_box[now.first][now.second]+1;
                        }
                    }
                }
            }
                  
            int days = -1;
            for (int i = 1; i <= N ; ++i){
                for(int j = 1 ; j <= M ; ++j){
                    if (grid_orange_box[i][j] == 0){
                        cout << "No answer: -1" << endl;
                        return 0;
                    }
                    if (grid_orange_box[i][j] > days){
                        days = grid_orange_box[i][j];
                    }
                }
            }
                  
            cout << "Answer: " << (days-1) << endl;
            return 0;
        }
      

4-3. DFS 연습문제

• DFS(Depth First Search, 깊이우선탐색)
  • 즉시 노드를 방문 (탐색 X)
  • 스택(stack)을 사용하여 문제 해결
  • 스택(stack)은 Last In First Out의 데이터 배열 자료구조를 말해요
  • 스택(stack)의 역할은 지금까지 방문한 노드를 모두 저장하는 역할을 합니다. (Trace)

  • DFS는 스택 자료구조를 이용해서 문제를 풀게 됩니다. 사용할 함수 스택(call stack)에 대해 알아보아요.

  • 일반적인 함수 호출

            int main(){
                printf("-143의 절대값은: ?%d\n", abs(-143));
            }
  

  • 호출순서: main → printf → abs
  • 종료순서: abs → printf → main

  

  • 재귀함수(recurrent) 호출

            inf f(int n){
                if (n==1) return 1;
                return f(n-1)*n;
            }
            int main(){
                int res = f(4);
                printf("Factorial(4): %d\n", res);
            }
  

  • 호출순서: f(4) → f(3) → f(2) → f(1)

  • 종료순서: f(1) → f(2) → f(3) → f(4)

  • 
• 아파트 단지를 식별하라 ( DFS 문제)

  • 문제 설명:

    

  • 문제 풀이: 아래와 같이 배열을 식별할 수 있으면, 인접한 모든 아파트를 단지로 식별할 수 있다.

    

    • STEP에 따른 좌표 탐색 호출 순서
    • 현재 방문 좌표를 (⭐)로 표시

      1. 시작점(1,1)

         (1,1) 좌표에서 DFS 함수 호출

      2. (-1,0) 이동하여 (0,1) 방문

         더 이상 갈 수 있는 곳이 없음

      3. (1,1)로 돌아옴

         

      4. (0,1)이동하여 (1,2) 방문

         그 다음 이동할 수 있는 공간 존재

      5. (1,0)이동하여 (2,2) 방문

         그 다음 이동할 수 있는 공간 존재

      6. (0,1)이동하여 (2,3) 방문

         그 다음 이동할 수 있는 공간 존재

      7. 계속해서 이동할 수 있는 공간으로 이동 …

         더 이상 이동할 수 있는 공간 없음

      8. 이전 지점을 돌아감 (호출 스택에서 제거됨)

      9. (2,2) 지점에서 갈 수 있는 지점 발견하여 이동 (3,2)

         

      10. 더 이상 갈 수 있는 공간 없으므로 이전 지점으로 돌아감 (호출 스택에서 제거됨)

      11. (1,1) 지점에서 갈 수 있는 지점 발견하여 이동 (1,0)

          더 이상 갈 수 있는 곳 없음

      12. 더 이상 갈 수 있는 공간 없으므로 이전 지점으로 돌아감 (호출 스택에서 제거됨)
      13. 스택에서 모든 것이 제거됨
      14. 깊이 노드의 끝까지 탐색 완료

    • DFS 함수의 프로토타입 형태:

      

      • 다음 지점의 좌표가 범위를 벗어나거나, 이미 방문한 곳이거나, 유효하지 않은 조건이라면 DFS 재귀함수 호출 없이 종료되고, 그렇지 않은 경우 MAP[x][y]를 특정값으로 식별

  • 문제 구현:

      #include <iostream>
      #include <vector>
      #include <algorithm>
            
      using namespace std;
      int N;
      void DFS(int x,int y);
      vector<vector<int>> grid(30, vector<int>(30,0));
      int cnt = 1; // 단지마다 번호를 세기 위함
            
      vector<int> ap(900,0); // 단지마다 몇개 아파트가 속해 있는지 개수를 세기 위함
      vector<pair<int,int>> delta = { {1,0}, {-1,0}, {0,1}, {0,-1} };
            
      int main(){
          // ------|check the result| ------
          cin >> N;
          for(int i =0 ; i < N ; ++i){
              string row ;
              cin >> row;
              for(int j =0 ; j < row.length() ; ++j){
                  grid[i][j] = row[j]-'0';
              }
          }
          // ------|solution|------ 
          for(int i = 0 ; i < N ; ++i){
              for(int j = 0 ; j < N ; ++j){
                  if (grid[i][j] == 1){
                      // cnt가 2부터 시작하는 이유: grid에 '1'이라는 정보가 이미 '아파트가 있음'을 알려주는 정보로 사용되고 있기 때문
                      cnt += 1;
                      // ------|dfs calling|------
                      DFS(i,j); 
                  }
              }
          }
          // ------|check the result|------
          cout << endl << "APART Complex:" << cnt-1 << endl;
          for(int i = 0 ; i < N ; ++i){
              for(int j =0 ; j < N ; ++j){
                  cout << grid[i][j];
              }
              cout << endl;
          }
          // ------|답 출력을 위한 구문|------
          sort(ap.begin()+2, ap.begin()+cnt+1); // 오름차순 정렬
          cout << cnt-1 << " ";
          for(int i =2 ; i <= cnt ; ++i){
              cout << ap[i] << " ";
          }
          return 0;
      }
            
      void DFS(int x,int y){
          grid[x][y] = cnt;
          ap[cnt] +=1;
          for(auto d : delta){
              int nx = x + d.first;
              int ny = y + d.second;
              if (!(nx >= 0 && nx < N && ny>=0 && ny <N))
                  continue;
              if (!(grid[nx][ny]==1))
                  continue;
              DFS(nx, ny);
          }
          return;
      }
    

• 욕심쟁이 딸기쟁이 조이 (DFS+DP 결합문제)

  • 문제 설명:

      Q) 조이는 nxn의 크기의 딸기밭을 방문했다. 조이는 딸기밭의 딸기를 수확할 수 있는데,
      어떤 지역에 있는 딸기를 모두 수확하면 상,하,좌,우 중 한 곳으로 이동을 하고, 그곳에서 딸기를 수확한다.
            
      그런데, 이 조이는 욕심이 많아서 딸기를 수확하고 자리를 옮기면, 새로 도착한 지역에 전 지역보다 딸기가 많아야 한다.
      조이는 어떤 지점에서 수확을 시작하여야 최대한 많은 칸을 방문하여 수확할 수 있는지 고민에 빠져 있다.
      조이를 도와주는 프로그램을 작성하여라
            
      첫 줄에 딸기밭의 크기 n (1<=n<=500)이 주어지고, 둘째 줄부터 n+1번째 줄까지는 딸기밭의 정보가 주어진다.
      딸기밭의 정보는 공백으로 구분되며, 각 지역의 딸기의 양의 정수로 주어진다.
      (단, 딸기의 양은 1,000,000보다 작거나 같은 자연수이다.)
            
      위와 같은 입력이 주어질 때, 조이가 최대로 이동할 수 있는 횟수를 출력한다.
    

    

  • 문제 풀이:
    • DFS 를 써서 문제를 풀 수 있다. 유효한 경로가 가장 긴 녀석의 개수가 본 문제의 답이 된다.
    • 그러나, DFS만으로만 문제를 풀면 모든 지점에 대하여 DFS알고리즘이 작동하여 함수의 실행 횟수 (호출 스택)이 많이 늘어나, 비효율적인 코드가 된다.

    • 비효율을 방지하기 위한 DP 프로그래밍 기법을 활용하여 전체 코드의 실행시간을 줄이자.

      • DP 프로그래밍은 점화식을 이용하여 푸는 문제로, 이전 스텝의 출력값을 배열에 저장하고, 현재 스텝의 출력값은 이전 출력값과 관계식(점화식)을 이용하여 현재 스텝의 출력값을 구함으로써, 반복 계산을 줄일 수 있다.

      • 이런 특징을 메모이제이션(memoization)이라 한다.

    1. DFS함수 사용
       • 모든 지점에 DFS 함수를 호출하고 (아파트 문제와 동일)
       • 확산 조건(유효조건): 현재 위치의 딸기 개수 < 다음 위치의 딸기 개수
    2. DP 를 이용하여 연산 횟수 줄이기
       • Top-down 접근: 동적 프로그래밍 적용
       • 메모이제이션(memoization)

       

    3. DFS와 DP 결합하여 문제 풀이

       

  • 문제 구현:

      #include <iostream>
      #include <vector>
      #include <algorithm>
      // DFS로 각 노드들의 최대 깊이를 구한다.
      // DFS가 반복된 계산을 하는 비효율을 줄이기 위해 Dynamic Programming을 설계해준다. (Memoization)
            
      using namespace std;
      int n;
      vector<vector<int>> strawbery(510, vector<int>(510,0));
      vector<vector<int>> DP(510, vector<int>(510,0));
            
      vector<pair<int, int>> delta = { {-1,0},{1,0},{0,-1},{0,1} };
      int DFS(int x, int y);
            
      int main(){
          cin >> n;
          for(int i = 0 ; i < n ; ++i){
              for(int j =0 ; j < n ; ++j){
                  cin >> strawbery[i][j];
              }
          }
            
          // --------------- |DFS calling| ----------------------
          for(int i=0 ; i<n ; ++i){
              for(int j=0 ; j<n ; ++j){
                  //memoization 계속해서 불필요한 DFS 함수 호출이 되지 않게끔
                  if (DP[i][j] == 0)
                      DP[i][j] = DFS(i,j);
              }
          }
            
          int answer = -1;
          cout << endl <<"DP 배열:\n";
          for(int i = 0 ; i < n ; ++i){
              for(int j =0 ; j < n ; ++j){
                  cout << DP[i][j] << " ";
                  if (answer < DP[i][j])
                      answer = DP[i][j];
              }
              cout << endl;
          }
            
          cout << endl << "ANSWER: " << answer << endl;
          return 0;
      }
            
      int DFS(int x, int y){
          //memoization 계속해서 불필요한 DFS 함수 호출이 되지 않게끔
          if (DP[x][y] != 0)
              return DP[x][y];
                
          for(auto d : delta){
              int nx = x + d.first;
              int ny = y + d.second;
            
              if (!(nx>=0 && nx < n && ny>=0 && ny < n))
                  continue;
                    
              if (strawbery[x][y] < strawbery[nx][ny])
                  DP[x][y] = max(DP[x][y], DFS(nx,ny)+1);
          }
          return DP[x][y];
      }
    

5. 레퍼런스

1. 위키독스(프로그래밍 온라인 교재)

   점프 투 파이썬

2. 프로그래머스(알고리즘 문제)

   코딩테스트 연습

6. 연습문제

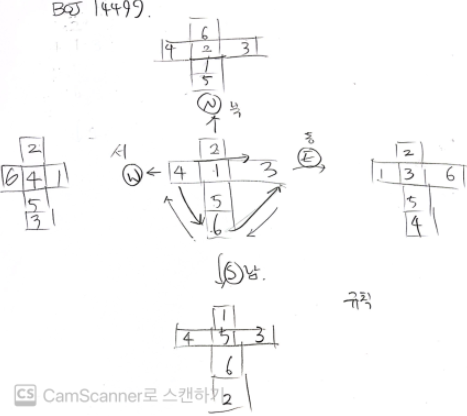
6-1. BOJ 14499(구현)

14499번: 주사위 굴리기

• 3차원을 머리속에서 굴리려니까 쉽지 않다.
  • 주사위가 회전하면서 바뀌는 동서남북 이동할 때의 주사위 순번을 덱에 담아서 어떻게 저쩌게 해보려고 햇는데, 틀렸고…, 생각을 해보니, 규칙이 틀린듯 싶다.
  • 그래프 자료구조를 써서 인접리스트를 만들어야하는건가.. 하고 있었는데, 그것까지는 아닌듯하다.
• 주사위 회전에 따른 면 배치 규칙을 손으로 그려보고 나서야 규칙을 찾고 풀 수 있었다.
  • 
• 제출 코드(c++)

        #include <iostream>
          
        using namespace std;
          
        int N, M;
        int x, y;
        int K;
          
        int map[21][21];
        int order[1001];
          
        int dice[7] = {0, 1, 2, 3, 4, 5, 6};
        int value[7] = {0, 0, 0, 0, 0, 0, 0};
          
        int main()
        {
          
            cin >> N >> M >> x >> y >> K;
            for (int i = 0; i < N; ++i)
                for (int j = 0; j < M; ++j)
                    cin >> map[i][j];
            for (int i = 0; i < K; ++i)
                cin >> order[i];
          
            pair<int, int> cur = {x, y};
          
            for (int i = 0; i < K; ++i)
            {
                bool in_map = false;
                switch (order[i])
                {
                case (1):
                    if (cur.second + 1 < M)
                    {
                        in_map = true;
                        cur.second += 1;
                        int temp = dice[6];
                        dice[6] = dice[4];
                        dice[4] = dice[1];
                        dice[1] = dice[3];
                        dice[3] = temp;
                    }
                    break;
                case (2):
                    if (cur.second - 1 >= 0)
                    {
                        in_map = true;
                        cur.second -= 1;
                        int temp = dice[6];
                        dice[6] = dice[3];
                        dice[3] = dice[1];
                        dice[1] = dice[4];
                        dice[4] = temp;
                    }
                    break;
          
                case (3):
                    if (cur.first - 1 >= 0)
                    {
                        in_map = true;
                        cur.first -= 1;
                        int temp = dice[6];
                        dice[6] = dice[5];
                        dice[5] = dice[1];
                        dice[1] = dice[2];
                        dice[2] = temp;
                    }
                    break;
          
                case (4):
                    if (cur.first + 1 < N)
                    {
                        in_map = true;
                        cur.first += 1;
                        int temp = dice[2];
                        dice[2] = dice[1];
                        dice[1] = dice[5];
                        dice[5] = dice[6];
                        dice[6] = temp;
                    }
                    break;
                }
          
                if (in_map)
                {
                    if (map[cur.first][cur.second] == 0)
                    {
                        map[cur.first][cur.second] = value[dice[1]];
                    }
                    else
                    {
                        value[dice[1]] = map[cur.first][cur.second];
                        map[cur.first][cur.second] = 0;
                    }
                    cout << value[dice[6]] << endl;
                }
            }
          
            return 0;
        }
  

6-2. BOJ 11053: LIS (DP)

11053번: 가장 긴 증가하는 부분 수열

• dyanamic programming 문제가 항상 어렵다.. 대표문제격인 LIS 문제를 풀어보자.
• LIS는 주어진 배열중에 숫자가 증가하는 규칙으로 숫자를 뽑았을 때 가질 수 있는 최장길이를 말한다.
  • 예: {1,7,2,4,9} 일 때, 최장길이는 4가 된다. (배열: {1,2,4,9})
• 풀이방법
  1. DP배열 정의: DP[i] : i번째 수를 끝 수로 하는 최장길이의 개수
  2. 점화식:if (arr[k] < arr[i]) DP[i] = max(DP[k] + 1, DP[i])
  3. 초기값: DP[0~n] = 1 최악의 경우에는 자기 자신이 최장길이의 개수가 된다.
• 코드

        #include <iostream>
        #include <vector>
          
        using namespace std;
          
        int main(){
            int N = 5;
            vector<int> A = {1,7,2,4,9};
          
              
            vector<int> DP(N,1);
            for(int i = 0 ; i < A.size(); ++i){
                for(int k = 0 ; k < i; ++k){
                    if (A[i] > A[k]) DP[i] = max(DP[k]+1, DP[i]);
                }
            }
          
            cout << DP[N-1] << endl;
        }
  

6-3. 프로그래머스 도둑질 Lv4(DP)

코딩테스트 연습 - 도둑질

• (220422 첫시도) 실패
  • DP 배열을 하나 잡고서 풀려고 시도했다.(LIS 풀이방식과 유사하게 접근) 주어진 테스트케이스는 맞추었으나, 채점 결과 점수가 대부분 틀리게 나왔고, 생각을 해보니 첫번째 집을 털 경우에 끝집을 털면 안되는데, 아래 코드는 그런 부분에 대해서 처리가 안되어 있다.

        int N = money.size();
              
            for(int i = 0 ; i < N ; ++i){
                DP[i] = money[i];
                  
                for(int k =0 ; k<i ; ++k){
                    if (abs(i-k) > 1 ){ //이웃의 집은 털지 못하게
                        DP[i] = max(DP[i], DP[k]+money[i]);
                    }
                }
            }
  

• 풀이방법(DP배열을 2개 잡아서 풀어야한다)
  • 고민을 꽤 오래 해보았는데, 답이 떠오르지가 않아.. 다른 사람 풀이를 참고해보니, 배열을 한개가 아닌, 두개를 잡고 동적프로그래밍을 풀었더라.
    1. 첫번째 집을 털 경우에 대한 배열: DP1
       • 첫번째 집을 털 경우엔 자동으로 끝에 집을 털 수 없다.
    2. 첫번째 집을 털지 못한 경우에 대한 배열: DP2
       • 첫번째 집을 털지 않았으니, 끝에 집을 털 수 있다.
  • DP 배열 정의
    1. DP1[n] = 첫번째 집을 털었고, n번째 집까지 왔을 때, 털 수 있는 돈의 최대값
    2. DP2[n] = 첫번째 집은 털지 않았고, n번째 집까지 왔을 때, 털 수 있는 돈의 최대값
  • DP 초기값 정의
    1. DP1[0] = money[0] , 첫번째 집을 털었다. DP1[1] = money[0], 두번째 집은 털지 못한다.
    2. DP2[0] = 0, 첫번째 집을 털지 않았고, DP2[1] = money[1], 두 번째 집은 털었다.
  • 점화식
    • if (i != N-1) DP1[i] = max(DP1[i-2] + money[i] , DP1[i-1]); DP2[i] = max(DP2[i-2]+money[i], DP2[i-1]);
    • 최종적으로 답을 구할땐, DP1과 DP2 두 개에 담긴 값중 최대값을 리턴한다.
      • return max(DP2[N-1], DP1[N-2]);

• 제출코드(c++)

        #include <string>
        #include <vector>
        #include <iostream>
          
        using namespace std;
          
        int solution(vector<int> money) {
            int answer = 0;
              
            int N = money.size();
            vector<int> DP1(N,money[0]); //첫번째 집 털었을 때,
            vector<int> DP2(N,money[1]); //첫번째 집 못 털었을 때,
            DP2[0] = 0;
          
            for(int i = 2 ; i < N ; ++i){
                if (i != N-1) DP1[i] = max(DP1[i-2] + money[i] , DP1[i-1]);
                DP2[i] = max(DP2[i-2]+money[i], DP2[i-1]);
            }
          
            return max(DP2[N-1], DP1[N-2]); //DP1과 DP2에 담긴 값중 최대값을 리턴
        }
  

6-4. BOJ 23291(구현)

23291번: 어항 정리

• 구현 문제 (아래 포스팅에 잘 정리해놓은 듯 하다.)
  • [BOJ] 백준 23291 어항 정리 포스팅
  • 구현문제는 class를 만들어 푸는 것이 좋다.
  • 어항쌓는 규칙 찾는 것에서 고민하다가 직접 구현 않고, 포스팅 참고함

        class solver;
        int main(){       
        	   solver solve_this();
               while (1)
               {
                      solve_this.addFish();           // 1. 물고기 추가
          
                      solve_this.roll();              // 2. 어항 쌓기
                      solve_this.controlFish();       // 3. 물고기 수 조절
                      solve_this.sortFish();          // 4. 물고기 정렬
          
                      solve_this.fold();              // 5. 어항 접기
                      solve_this.controlFish();       // 6. 물고기 수 조절
                      solve_this.sortFish();          // 7. 물고기 정렬
          
                      ans++;                          // 8. 정리 횟수
                      if (solve_this.getDiff() <= K) break;
               }
               printf("%d\n", ans);
  

끝