Path
Search as A* & D*
Motion Planning - AStar & DStar
2022-02-01 10:10
Search algorithm: A star & D star
AUTHOR: Sungwook LE
DATE: ‘22.2/01
Code: My Code A*
Reference:
1. A* Introduction
-
A star algorithm은 효율적인 최단거리 길찾기 알고리즘으로, autonomous parking system에서 쓰인다.

-
위의 구조에서
CellSort(), ExpandNeighbors(), CheckValidCell(), Heuristic(), AddToOpen()method가 A Star 알고리즘의 전부이다. -
CellSort()이름을 통해 전체 알고리즘의 대략적으로 설명해보자.Cell은 현재 지도의 좌표(2차원 격자)를 의미한다.Cell을Sort한다는 의미는Cell이 가지고 있는 어떤 Cost Value를 정렬한다는 의미이다. -
A*알고리즘의 Cost Function은 $f = g + h$ 이다. g는 출발지 부터 해당 cell까지의 경로 거리를 의미하고, h는 목적지로부터 해당 cell까지의 경로 거리를 의미한다. heuristic value인h는 다양한 방식으로 변형이 가능하다.
- 앞에서 기술한 바와 같이,
A star는 Cost Value와 Cost Value에 따른 Sort를 통한 선택이 가장 핵심이 되는 부분이다.- $Cost \space value, \space f = g + h$
- $g$는 출발점으로 부터 현재 cell까지의 발생한 이동 경로 거리를 의미한다.
- 이번 구현에서는 heuristic value $h$를
Manhatan distance로 목적지로부터 타겟cell의 거리로 하였다.int manhatan_dist(std::vector<int> target, std::vector<int> goal){ int res; res = std::abs(goal[0]-target[0]) + std::abs(goal[1]-target[1]); return res; } - 구해진 $cost \space value$를 기준으로 Cell을 Sorting하고 선택(
pop_back)한다.
2. A* 구현
- 이번 구현에서는
maze.txt를 입력받아 지도로 사용하므로 전체 코드에는ReadBoardFile()이 존재하고, 찾은 경로를 출력해주는PrintSolution()가 있으나,Search()알고리즘에 포커싱하여 살펴보자 - 핵심이 되는
Search알고리즘은 다음과 같다.
2-1. A* 코드(C++)
void A_star::initialize(){
closed[start[0]][start[1]] = 1; // closed
heauristic_calculate();
x = start[0];
y = start[1];
g = 0;
h = heuristic[x][y];
f = g+h;
opens.push_back({f,h,x,y});
found = false;
resign = false;
count = 0;
}
std::vector<std::vector<std::string>> A_star::Search(){
A_star::initialize();
while (found != true && resign != true)
{
if (opens.size() == 0)
{
resign = true;
navigation[start[0]][start[1]] = "S";
navigation[goal[0]][goal[1]] = "G";
std::cout << "Fail to find the exit!" << std::endl;
break;
}
else
{
// CellSort()
std::sort(opens.begin(), opens.end(), [](auto a, auto b)
{
if (a[0] > b[0])
return true;
else
return false; });
next = opens.back();
opens.pop_back();
f = next[0];
g = next[1];
x = next[2], y = next[3];
count_traced[x][y] = count;
count += 1;
if ((x == goal[0]) && (y == goal[1]))
{
found = true;
// SAVE NAVIGATION
navigation[x][y] = "*G";
while ((x != start[0]) || (y != start[1]))
{
int x_ex = x - delta[delta_traced[x][y]][0];
int y_ex = y - delta[delta_traced[x][y]][1];
navigation[x_ex][y_ex] = delta_emoji[delta_traced[x][y]];
x = x_ex;
y = y_ex;
}
navigation[x][y] = "*S";
}
else
{
// ExpandNeighbors()
for (int i = 0; i < delta.size(); ++i)
{
int x2 = x + delta[i][0];
int y2 = y + delta[i][1];
// CheckValidCell()
if ((x2 >= 0) && (x2 < map.size()) && (y2 >= 0) && (y2 < map[0].size()))
{
if ((closed[x2][y2] == 0) && (map[x2][y2] == 0))
{
int g2 = g + cost;
int h2 = heuristic_map[x2][y2];
int f2 = g2 + h2;
// AddToOpen()
opens.push_back({f2, g2, x2, y2});
closed[x2][y2] = 1;
delta_traced[x2][y2] = i;
}
}
}
}
}
}
return navigation;
}
2-2. A* Results
MAP is:
* 1 0 0 0 0 0 0
0 1 0 1 1 1 1 0
0 1 0 0 0 0 1 0
0 1 1 0 1 0 1 0
0 1 0 0 1 1 1 0
0 0 0 1 1 0 0 *
** 1 is grid / 0 is aisle
NAVIGATOR is:
S* # > > > > > v
v # ^ # # # # v
v # ^ < # v
v # # ^ # # v
v # > ^ # # # v
> > ^ # # G*
COST is:
S -1 17 18 19 20 21 22
1 -1 16 -1 -1 -1 -1 23
2 -1 15 11 12 13 -1 24
3 -1 -1 10 -1 14 -1 25
4 -1 8 9 -1 -1 -1 26
5 6 7 -1 -1 -1 -1 G
** Number is cost value(how many step: 27)
2-3. 구현 결과
- A star 알고리즘은 아래 Flow를 기억하자
- 시작지점과 끝지점 그리고 MAP을 받아 초기화한다.
- Cell 마다 Heuristic Value를 계산해 둔다.
- 시작지점부터 주변의 Cell을 Neighbor(
상,하,좌,우)로 추가하고 Neighbor의 Cost Value(f=g+h)를 계산한다. - Cost Value가 계산된 Cell은
visited표시를 하여 중복 계산이 안되게끔 한다. - 제일 작은 Cost Value를 갖는 Cell을 다음 이동 지점으로 고르고 주변 Cell을 탐색한다.
- 더 이상 새로운 cell을 추가할 수 없을 땐, 길을 못 찾는단 의미이고 목적지에 도달하면 경로를 출력한다.
- Heuristic Value를 잘 선택하면 탐색 횟수를 줄일 수도 있을 것이고, 최악의 경우엔 모든 cell을 탐색해서라도 경로를 찾아내는 A star algorithm에 대해 리뷰하였다.
3. 학술적 정리: Search in Path Planning
- Find a path between two locations in an unknown, partially known, or know environment
- Uninformed Search
- Use no information obtained fron the environment
- Blind Search: BFS, DFS, Dijkstra
- Informed Search
- Use evaluation function, More efficient
- Heuristic Search: AStar, DStar, etc..
3-1. A* algorithm Flow Chart
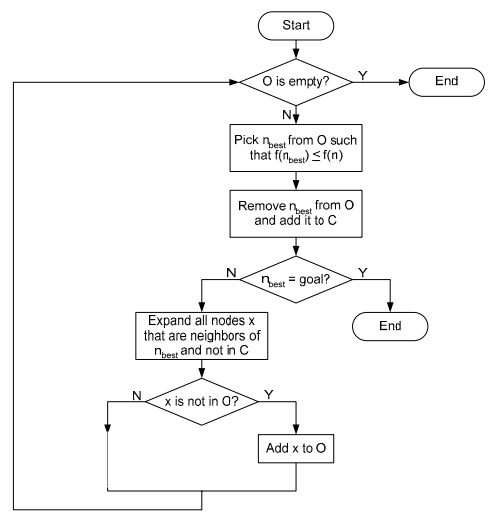
- Open list(O) stores nodes for expansions
- 방문하지 않은 노드에 대해서 현재 위치의 이웃 노드를 Open list에 추가
- Closed list(C) stores nodes which we have explored
- 방문한 노드는 Closed/Visited 체크
- A*는 Optimal path planning이 가능함
- 참고: Dijkstra’s Search는 f(n) = g(n) 인 케이스, Total Cost $f$를 이동경로에 대한 비용 $g$만 따져서 경로 Search, heuristic 값을 사용치 않음
3-2. A* Star Replanner
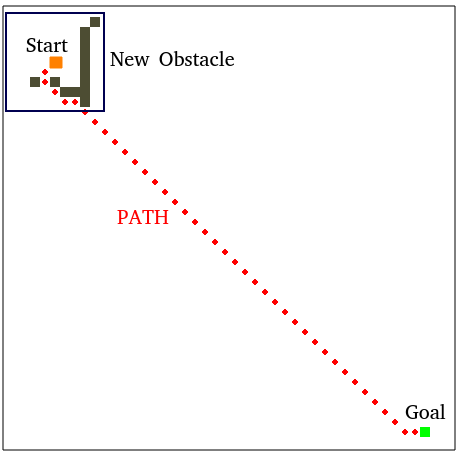
- A Star Replanner: 새로운 맵(장애물) 정보가 들어오면, 그 지점을 시작점으로 하여 A* 알고리즘 재수행
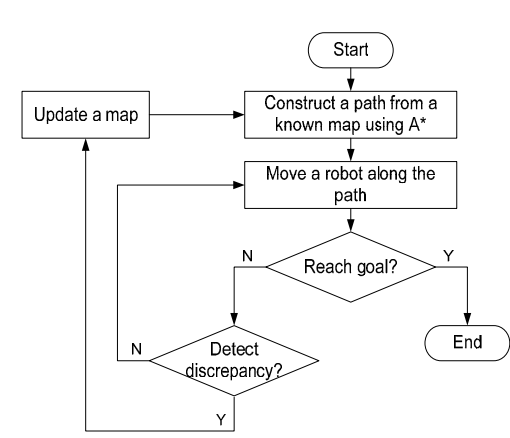
- Optimal but, Inefficient and impractical..!
- DStar(Dynamic AStar) 등장 이유, 동적인(partially known, unknown map) 환경에서 효율적인 길찾기 알고리즘(재수행)
4. D* Lite Introduction
- Based on A*, there are various version of DStar(Dstar, Focused DStar, DStar Lite…)
- Incrementally repair solution paths when changes occur -> Fast replanngin
- DStar(Dynamic AStar) 등장 이유, 동적인(partially known, unknown map) 환경에서 효율적인 길찾기 알고리즘(재수행)
- 왜 효율적이냐, InConsistent한 Node만을 Openlist에 추가하고, 탐색함으로써 새로운 장애물/맵정보가 들어왔을때 영향을 받는 Node만을 대상으로 길찾기 알고리즘 재수행이 가능
4-1. terminology
- $g$: the objective function value
- $rhs$: the objective function value of one-step lookahead
- “Consistency”
- Consistent => $g=rhs$
- Inconsistent => $g!=rhs$
- Inconsistent nodes go on the open list
- “b” is a successor of “a” and “a” is a predecessor of “b”
- $rhs$ value of a node is computed based on the $g$ values of its sucessors in the graph and the transition costs of the edges to those successors.
- $rhs(u) = min_{s’~in~successor(u)}{(c(u,s’)+g(s’))}$
- The key(priority) of a node on the open list is the minimum of its $g$ and $rhs$ values plus a focusing heuristic, $h$.
- $[min(g(s), rhs(s))+h(s_{start},s);~min(g(s), rhs(s))]$
4-2. D* Lite Algorithm


- CMU AStar & DStar Matrial 자료의 p75~p131 의 예제 문제를 따라가며 살펴보자!!